
Response to Wytze P. Oosterhuis—analytical performance specifications in clinical chemistry: the holy grail?
Introduction
Recently in this journal, Oosterhuis (1) lamented how there was no consensus on how to deal with two important issues as they relate to performance specifications based on biological variation:
Measurement uncertainty (MU) which excludes reproducible bias but includes the uncertainty of bias, and;
The model for permissible (or allowable) total error (TEa or pTAE) which includes bias but overestimates TE because maximum values for imprecision and bias are incompatible.
He also described that challenges remain to integrate the different concepts, both for the definition of performance and of performance specifications as for quality control procedures.
In this paper we will present our solution to these problems which started with a discovery by one of the current authors (MA Mackay), who developed this into a simple practical technique for QC target setting and performance assessment. The original technique has been in use ever since, in laboratories associated with the inventor, passing all accreditation to ISO 17025 and ISO 15189.
We have spent the last few years developing a theoretical basis for the technique (2-4) and have described new concepts: SEdrift, steady state errors, and the Reference Change Factor. We suggest that our model is a candidate “model that is both useful and as less flawed as possible” to use the expression of Oosterhuis (1).
Original technique and its development
The technique was developed for performance planning and assessment in order to simplify management of an error budget, but it is very similar to how performance specifications are calculated. The original discovery was to find that imprecision of APS/4, APS/5 and APS/6 with drift of APS/8 each met a 5% error budget if used with a matching QC algorithm i.e., one that delivered 90% Ped at that level of imprecision. This set standard ‘grades’ for imprecision performance. APS/8 was used as a drift allowance, i.e., there was a need to check that assay drift was ≤ APS/8. If APS was set to CVi, there was great similarity to a proposed Biological Variation model (5) where optimal imprecision was CVi/4. The difference being a drift component based on CVi rather than a bias component based on CVg.
The technique was called Assay Capability, defined as Cpa = APS/SDa (= APS/CVa) which described the number of SD inside the APS. Assays were classified by performance grade based on imprecision (Cpa <4, 4–5, 5–6 and >6) which could then be used to develop QC policy around these grades e.g., matching QC algorithm, rerun policy, etc.
To be truly useful, it was essential that this QC technique work on EQA data to show achievable peer performance. Ten continuous cycles covering several years [1995–1998] of the RCPAQAP General Serum Chemistry program (6), each cycle with >50 measurands and 400 to 500 participants, were examined. The technique worked consistently and well.
Initial/preliminary analysis found the technique worked with many other RCPAQAP programs over that period (e.g., lipids, neonatal bilirubin, antibiotics, special drugs, endocrine, tumour markers, general urine, urinary metanephrines). Participant numbers were smaller in some programs and results have not been reported in peer reviewed literature.
Because some assays perform so poorly even the best laboratories cannot meet an error budget, a 3×3 grid or matrix of achievable imprecision (top 20th percentile EQA) versus laboratory imprecision was developed. Grid boundaries were set at Cpa 4 and Cpa 6, because when the 20th percentile laboratory participant had imprecision of Cpa 6, 50–80% of all participants achieved Cpa 4, i.e., imprecision satisfied an error budget (7). This 3×3 grid was used to summarise the performance of all assays in an EQA cycle in one diagram. Independently of RCPAQAP, the 3×3 was trialled as an end of cycle summary for the RCPAQAP Hitachi instrument user group of 45 laboratories for one general chemistry cycle in 1997.
Several colleagues in the inventor’s laboratories were enthusiastically involved in developing a comprehensive QC system around the performance classes, enhancing the technique and the 3×3, deploying and promoting them.
We recently examined nine current common chemistry cycles covering 7 years [2010–2016] and each cycle with >600 participants, to show the technique still applies. This was documented, but only by extending the 3×3 grid to produce a risk model (2), which has proved to be rudimentary compared to our later work.
In our second recent publication (3) we validated the drift component which we termed SEdrift, showed how Ped declined as drift increased, put forward a new error budget diagram to specifically include method drift, and showed how SEcrit can be calculated from APS, Cpa and SEdrift.
The third paper (4) used Cpa and SEdrift in a normal distribution to calculate the error rate at steady state and inverted this error rate to produce a normalised QC run length. We suggested that a functional run length could be calculated by multiplying by the Ped of the QC algorithm at the calculated critical shift. In effect a critical shift causing 5% errors would be detected within the average number of samples containing one steady state error. We noted that this was analytical risk for an analytical APS, that some APS may be arbitrarily set e.g., by regulators and that there were different APS for patient diagnosis and monitoring. We suggested that clinical risk required a clinically relevant APS.
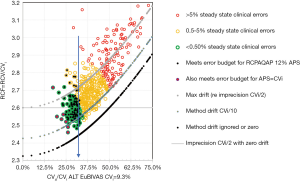
Our latest work extends the technique to RCV finding that performance grades or boundaries could be defined at fixed ratios of CVi. RCV/CVi =2.7 was a practical upper limit for the shift to detect a significant change at 95% in one direction (increase/decrease) and 90% in both directions, while assays meeting a 5% clinical error budget could detect this change at RCV/CVi ≤ 2.5 only if drift was ≤ CVi/10. These two levels are performance boundaries focussed on CVi, not CVa, and so are a metric for comparing laboratory performance. The results suggested that imprecision of CVi/2 was a minimum for a stable assay, because combined with drift of CVi/10, RCV/CVi =2.7 (see Figure 1). These findings demonstrate that the ratio RCV/CVi plays an important role in defining these boundaries, hence we have defined this as the reference change factor (RCF).
We believe these publications advance the discussion, metrics and measurement of analytical and clinical Risk in clinical laboratories. This approach to risk is evidence based because it has a theoretical basis, meshes the concepts of QC and EQA, and is supported by QC, EQA and CVi data, and above all is implementable.
The issues raised by Oosterhuis
In the rest of this article we shall respond to some of the issues raised by Oosterhuis (1) and how our model has addressed these.
Bias (definition of bias and imprecision)
Oosterhuis commented that: “Bias proves to be a difficult concept. GUM defines bias as any error that is reproducible, without defining the time frame. …. One can distinguish between short-term bias (e.g., within day, one shift) and long-term bias (e.g., during several weeks or months): many effects causing short-term bias, e.g., re-calibrations may be seen as bias within this short time frame but may be indistinguishable from random effects when variation is observed over a longer time period.”
Systematic method bias is reproducible, the difference between monthly QC mean and its target is not. So SEdrift is not bias that should be excluded by GUM but is a component of variation to be included in MU.
The question is how should this be done? The answer is to look at the distribution for the period of estimating a QC mean and SD. In this context, SEdrift is a systematic error component that shifts a distribution, as shown in our error budget diagram (3).
If we look at a long term continuous selection of these periods, for which QC mean and SD are calculated, we can see we need to consolidate the multiple measurements of imprecision and of drift. Imprecision can be pooled, but this does nothing to address the drift. The scatter of the drift can be determined as the SD of each difference between the QC mean and the long-term target. This is how we calculate SEdrift. The scatter of the drift is included as the variable component of bias.
For MU, or comparing within a method group, the target should not include systematic method bias, just drift (SEdrift). Systematic method bias is an issue for comparing patient results between laboratories and requires commutable material with a target value traceable to a certified reference method and certified reference material.
Performance specifications and quality control limits
Oosterhuis: “Quality assurance limits will generally be stricter—e.g., by 1.65 SDa—than performance limits in order to maintain the performance goals and assure that—within a pre-defined probability—that these goals are achieved.”
Specifications are meant to relate to purpose, in this case a change in a result that defines a pathological process. Control limits relate to statistical limits of the measurement process. They are not the same.
It appears that the “performance specifications” as described by Oosterhuis are meant to act as a half-way point between clinical purpose and inadequate assays.
We suggest that instead of lowering the specifications for clinical purpose and accepting that assays are adequate, it is necessary to set a few levels to describe performance:
- Acceptable to distinguish from that requiring improvement;
- Target to identify what is a theoretically reasonable starting point for QC for acceptable performance;
- Achievable to identify that attained by a significant proportion of laboratories, and;
- Optimal as a boundary between acceptable and excellent (and so not inferring maximum theoretical performance or the best operationally).
Two older proposals put forward from different perspectives defined optimal performance and are compatible: analytically a 5% error budget, biologically imprecision of CVi/4.
The QC error budget technique was designed to restrict the level of errors to 5% when QC fails. It applies to any APS. A simple examination of QC algorithm Ped tells us that there are a few algorithms delivering 90% Ped of critical shifts when drift is APS/8. At this level of drift allowance, the minimum imprecision for an error budget is APS/4. This was the initial model and has been in use for over 20 years.
We now have more detailed analysis of why this model works and have extended its usefulness to create performance boundaries for analytical and clinical risk by examining the situation where APS = CVi, that is, patient monitoring.
Imprecision of CVi/4 is the optimal performance goal in the Biological Variation model of Fraser (8) which was designed to restrict analytical variation compared to BV. To put it another way, for patient monitoring, the clinical specification for imprecision is CVi, and imprecision of CVi/4 satisfies a clinical error budget, leaving a modest margin for drift—assuming constant systematic bias has been accounted for, for example by factoring.
Our recent work showed that an imprecision target alone or an error budget alone is insufficient to constrain steady state errors or RCF. Therefore, we have proposed targets or boundaries for both imprecision and drift alone, and for their combination, for which the best measures are steady state errors and RCF.
Six sigma and quality control perspectives
Oosterhuis: “the sigma scale with 6 as very good and 3 as just sufficient quality to maintain with quality control procedures.”
Long before 1990 it was recognised by Quality practitioners that 3 SD inside the tolerance limit did not account for drift and so the term for processes at this level of performance was changed from “capable” to “barely capable” (9).
Six Sigma is about error rates equivalent to imprecision alone within the APS. We use “Sigma” to refer directly to the level of imprecision not errors.
The error rates cited by Six Sigma are for a distribution based on imprecision alone being 6 SD inside the tolerance limit. But the operating situation is 4.5 sigma for imprecision and 1.5 Sigma for bias to account for drift (originally in batch manufacturing) (10).
We could add that the Six Sigma allowance for bias is near the maximum theoretically allowable as calculated by us and others (1,11,12). On the one hand, 1.5 SD is 25% of the APS; on the other hand, the ratio 1.5/4.5 is 33%. Bias at these levels severely hampers operational performance, either by reducing the error detection of the QC algorithm, by increasing steady state errors or by reducing the ability to detect patient changes, due to increasing RCF. At Target and Achievable performance method drift is half the level of imprecision, that is 0.5 SDa, not 1.5 SDa. Pathology may have an advantage because constant systematic error can be significantly reduced or removed from assays, and so the SE allowance is smaller.
Systematic error and imprecision combine differently in a normal distribution when calculating errors. Bias and method drift directly reduce the APS that must then be dealt with by imprecision.
We use separate metrics for imprecision and method drift; each is a multiple or fraction of the APS. When we say imprecision is 6 Sigma - we mean imprecision is APS/6. We can then combine the metrics to calculate errors using the normal distribution with APS as the boundary for an error.
Six Sigma is an example of grading the process; an excellent thing to do. But it is the process compared to specifications, i.e., a performance grade; not a specification for an APS which should be set for clinical use.
We note that Oosterhuis and Coskun (13) have promoted new sigma metrics, including CVi/CVa, which is the Assay Capability metric set specifically for patient monitoring. While this is a good thing, we have found that method drift cannot be ignored, so this metric is one of many contributing to understanding performance.
In pathology, imprecision is the major determinant in analytical errors, not drift, and not systematic bias which can be dealt with outside the measuring process itself. But high method drift can greatly reduce the ability to detect change in a patient.
Performance specifications based on biological variation or reference values?
“Although the contribution of the analytical variation to the total variation will in many cases be small, it is a simplification to assume that reference ranges are only determined by biological variation as has been done in many models.”
We have based our work on patient monitoring, not diagnosis. CVi is the APS and we have performance grades for imprecision, method drift, steady state errors and RCF.
So, we can detect an acceptably low analytical error rate when QC flags if the assay meets an error budget with a matching QC algorithm; from CVa = CVi/4, that is Cpa ≥4.
And we can calculate clinically significant changes in a patient and the risk of under- or over-reporting them using the reference change factor.
Why would we change this system that integrates and works so well to swap to “diagnosis” supposedly based on healthy individuals and where the performance expectations are less restrictive?
Combining MU and TE models
“In MU we only have the concept of the uncertainty of the measurement result.”
If so, then constant systematic bias has been omitted and is dealt with by traceability.
“The Task and Finish Group concluded that the MU model fits well for patients’ test results, while the TE model can be applied for quality control purposes.”
We have combined MU and TEa by calculating SEdrift as an SD (variability of method drift) and using it as a bias component in calculation (because that is how it acts).
“However, in patients there is no reference value and the result could be expressed with an estimate of the uncertainty.”
The reference value for patient monitoring is the APS which is CVi and for detecting significant changes there is the previous patient result.
RCV/CVi is a measure of the (minimum) uncertainty about a clinically significant change, for certain specific assumptions (for example, zero pre-analytical variation, stable CVi and CVa, etc).
Steady state error rate is a measure of the (minimum) analytical uncertainty of an assay when it’s “in control” (the assay can drift a little without this drift being detected, hence “minimum”).
“This still leaves open what error model to be used in quality control and how to determine quality limits. The bias concept still remains a problem, and we might even abandon the bias concept altogether and assume all forms of error (deviation from the reference value) as short- or long- term imprecision. We should be able to include in a model the maximum permissible difference between analysers performing the same test within one laboratory organisation.”
Parvin et al have demonstrated by simulation that what we define as SEdrift in a network should be calculated as the SD of the differences between the analyser mean and the long-term target mean set on the reference analyser (14). Using the reference mean for the QC rule reduces the risk of reporting unreliable patient results.
Conclusions
“The practice of the clinical laboratory is such, that it is impossible to describe performance specifications in a mathematically perfect model, and all models will be based on assumptions and can only approach complex reality. The challenge is to reach consensus on a model that is both useful and as less flawed as possible.”
Our model has proved useful for more than 20 years.
Now it is even more useful with a better understanding of the links between method drift, steady state errors, RCF and clinical risk.
Acknowledgments
Ken Worth, Gabe Hegedus, Leslie Burnett, Doug Chesher, Renze Bais and staff at the department of Clinical Chemistry at ICPMR, Westmead Hospital, the Biochemistry department of the Royal North Shore Hospital, Sydney, and all Pacific Laboratory Medicine Services networked laboratories.
Footnote
Provenance and Peer Review: This article was commissioned by the editorial office, Journal of Laboratory and Precision Medicine. The article has undergone external peer review.
Conflicts of Interest: Both authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/jlpm.2019.06.03). Tony Badrick serves as an unpaid editorial board member of Journal of Laboratory and Precision Medicine from January 2019 to December 2020. The authors have no other conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Oosterhuis WP. Analytical performance specifications in clinical chemistry: the holy grail? J Lab Precis Med 2017;2:78. [Crossref]
- Mackay M, Hegedus G, Badrick T. A simple matrix of analytical performance to identify assays that risk patients using External Quality Assurance program data. Clin Biochem 2016;49:596-600. [Crossref] [PubMed]
- Mackay M, Hegedus G, Badrick T. Assay Stability, the missing component of the Error Budget. Clin Biochem 2017;50:1136-44. [Crossref] [PubMed]
- Mackay MA, Badrick TC. Steady state errors and risk of a QC strategy. Clin Biochem 2019;64:37-43. [Crossref] [PubMed]
- Royal College of Pathologists of Australasia Quality Assurance Programs, St Leonards, Sydney. Available online: www.rcpaqap.com.au
- Fraser CG, Petersen PH. Desirable standards for laboratory tests if they are to fulfil medical needs. Clin Chem 1993;39:1447-53; discussion 1453-5. [PubMed]
- Stroobants AK, Goldschmidt HMJ, Plebani M. Error budget calculations in laboratory medicine: linking the concepts of biological variation and allowable medical errors. Clin Chim Acta 2003;333:169-76. [Crossref] [PubMed]
- Fraser CG. Quality Specifications in Laboratory Medicine. Clin Biochem Rev 1996;17:109-14.
- International Association for Six Sigma Certification (GOAL QPC). Available online: https://www.iassc.org/provider/goalqpc/. Accessed 1 April 2019.
- Harry MJ. Six Sigma: A breakthrough strategy for profitability. Quality Progress 1998;31:60-4.
- Fraser CG, Hyltoft Petersen P, Lytken Larsen M. Setting analytical goals for random error in specific clinical monitoring situations. Clin Chem 1990;36:1625-8. [PubMed]
- Larsen ML, Fraser CG, Petersen PH. A comparison of analytical goals for haemoglobin A1c assays derived using different strategies. Ann Clin Biochem 1991;28:272-8. [Crossref] [PubMed]
- Oosterhuis WP, Coskun A. Sigma metrics in laboratory medicine revisited: We are on the right road with the wrong map. Biochem Med (Zagreb) 2018;28:020503 [Crossref] [PubMed]
- Parvin CA, Kuchipudi L, Yundt-Pacheco J. Designing QC Rules in the Presence of Laboratory Bias: Should a QC Rule be Centered on the Instrument’s Mean or the Reference Mean? 2012. Poster at AACC meeting.
Cite this article as: Mackay MA, Badrick TC. Response to Wytze P. Oosterhuis—analytical performance specifications in clinical chemistry: the holy grail? J Lab Precis Med 2019;4:24.


